| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- layout
- 레이아웃
- Test
- Linked List
- AlignmentGuide
- hstack
- JavaScript
- 생각
- swiftUI
- Double Linked List
- 시계방향
- 각도
- optional binding
- 좌표공간
- Optional Chaining
- Universal Hashing
- 자료구조
- stack
- enum
- Optional
- vstack
- SWIFT
- nodejs
- Hashing
- Today
- Total
klioop for iOS
Memory 기초 본문
전체적인 큰 그림을 이해하기 위해 자세한 내용들은 제외되거나 생략되었습니다. 틀린 부분이 있다면 알려주세요.
메모리(Memory)
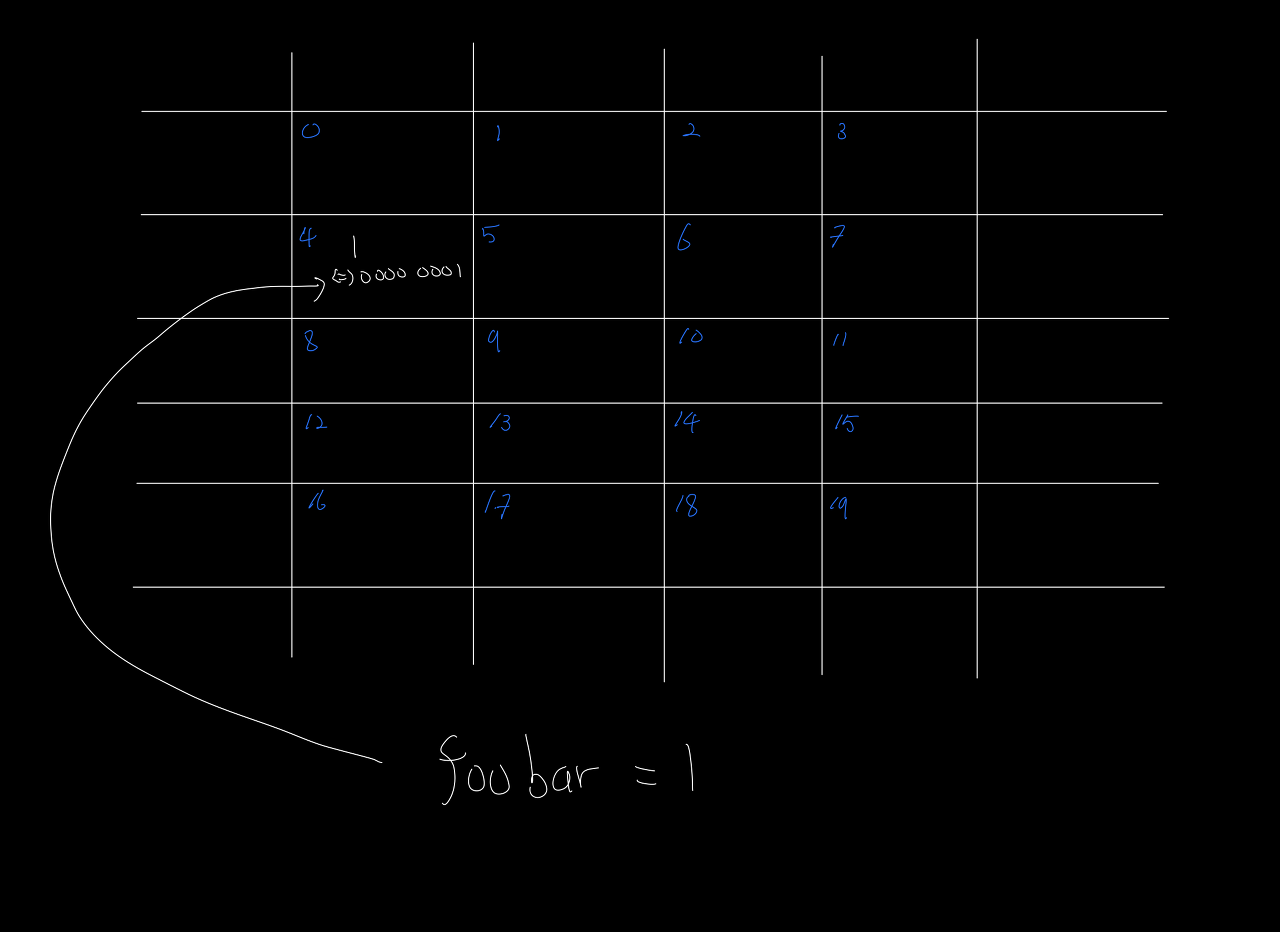
컴퓨터나 프로그램이 변수를 선언하면 컴퓨터는 그것을 어딘가에 저장해야 한다. 예를 들어, foobar = 1 선언하여 숫자 1 을 foobar 변수에 저장하려고 한다면, 이 1 은 컴퓨터 어딘가에 저장되어야 한다. 이 저장되는 장소가 주기억장치, 메모리다.
자세한 내용을 제외하고 Memory 를 그냥 크기가 한정된 하나의 캔버스 라고 생각하자. 그리고 그 캔버스에는 칸(slot) 들이 나눠져 있다.
아래에 그림 같이 생긴 저장소가 컴퓨터 어딘가에 살고 있다고 생각하자. 각 칸 들은 memory slot 이라고 불린다. 여기에서 이 캔버스의 크기가 한정되어(bounded)있다는 것에 주목해야 한다. 다시 말하면, memory slots 의 수는 제한되어 있다는 것이고 이는 memory 에 저장할 수 있는 데이터의 양은 무한하지 않다는 말과 같다.

알고리즘을 작성 할 때, Space complexity 가 중요한 이유다. Time complexity 가 동일할 때, 알고리즘이 사용하는 메모리 슬롯의 양이 적으면 적을 수록, 다른 용도를 위한 memory slots 이 많아지기 때문에 좋은 알고리즘으로 평가할 수 있다.
메모리에 저장되는 data 가 실제로 표현되는 방식, 0 과 1
그렇다면 실제로 data 가 메모리에 저장될 때는 어떠한 형태로 저장될 까?
또는 메모리에 저장하기 위해 우리가 사용 하는 unit 이 뭘까?
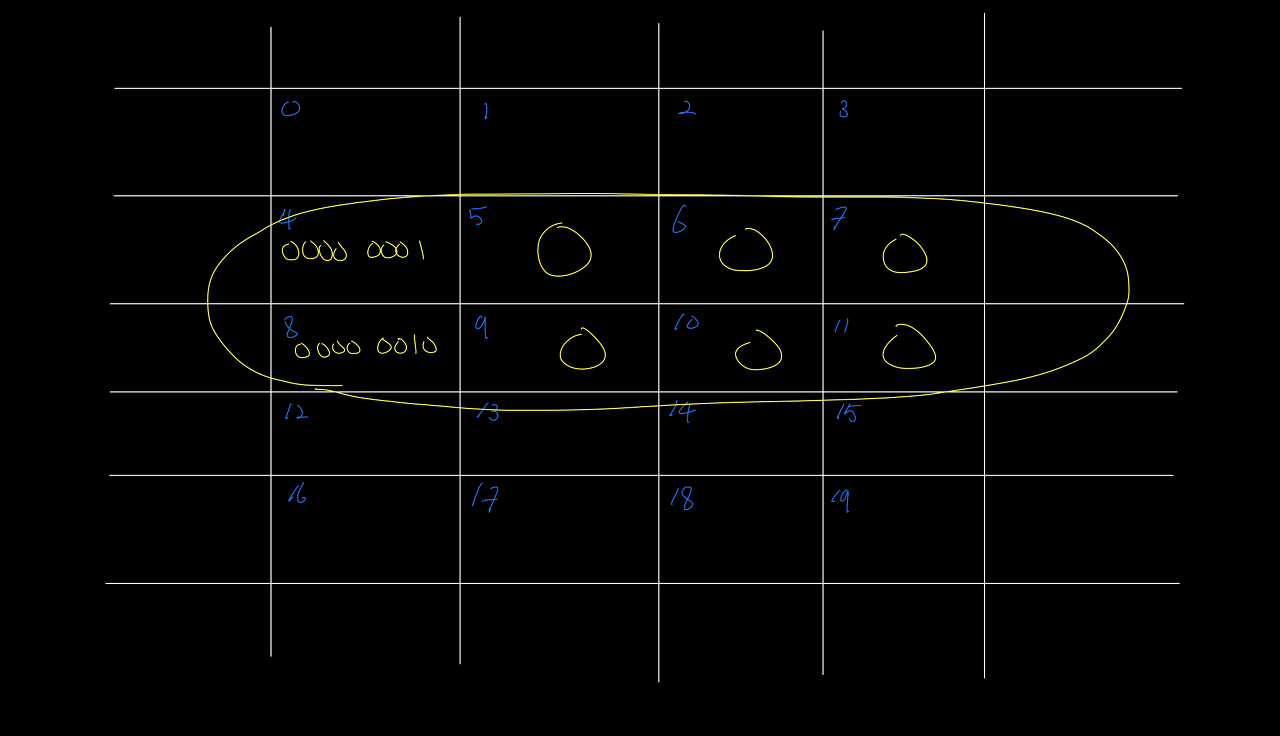
메모리의 데이터는 bits(binary digits), 즉 2 진수 0 과 1 로 저장된다. 그리고 하나의 메모리 슬롯은 8 bit, 또는 1 byte 의 정보만 담을 수 있고 정보를 저장하기 위해서는 아무것도 저장하고 있는 않은 상태(free)여야 한다. 앞에서 본 foobar 에 저장된 1 이 4 메모리 슬롯 에 저장된다고 하면, 비워져 있는 4 번째 슬롯에 숫자 1 이 그대로 저장되는 것이 아니라, 실제로는 0000 0001 이 저장된다.
그런데, 8-bits 는 최대 255(2^7 + ... 2^1 + 2^0) 의 수 까지 밖에 표현하지 못한다. 더 큰 수를 bits 로 저장하고 싶다면 어떻게 해야 할까?
단순히 수를 표현하는 bit 의 크기를 늘리면 된다.
실제로 우리가 컴퓨터로 다루는 모든 데이터는 0 과 1 로 변환이 가능하다. 예를 들어, Java 나 C++ 같은 언어에서는 type int 는 32-bit 정수를 나타내고 type long 은 64-bits 정수를 나타낸다. 여기서 중요한 점은, 우리가 정수를 다룰 때 고정된 너비의 정수(fixed-width integer)를 다룬 다는 것이다.
즉, 32-bits 정수로 정수를 다루기로 결정한다면(type int 로 정의한 수를 저장 한다면), 1 을 표현할 때도, 1000000 을 표현할 때도 32-bit 로 변환된다!
이는 다시, 32-bits int 로 1 을 저장하려면 메모리 슬롯이 4 개 필요하다는 말과 같다. 1, 200, 100000 모두 32-bits 로 다룬다면 우리는 언제나 하나의 수를 저장할 때 항상 4 개의 빈 슬롯이 필요하다는 것을 알고 있어야 한다는 말이다. 이 때, 단순하게 비워져 있는 슬롯 4 개가 아니라 연속적으로 비워져 있는 슬롯이 4개 필요하다(back to back free 4 slots).
1(32-bits) 을 저장하려고 하는데, 무슨 이유에서인지 5 번 슬롯이 어떤 정보를 저장하고 있다. 그렇다면, 1 은 8 bits 로 충분히 표현 가능하지만, 4번 슬롯에 저장되지 못하고 다른 슬롯에 저장되어야 한다. 저장되는 슬롯을 포함해서 4 개의 슬롯은 비워져 있어야 한다는 것이다.

List
숫자들을 가지고 있는 list 를 저장하고 싶을 때도 동일한 원리가 작동한다. 32bits 정수 1 과 2 를 가지고 있는 이 리스트, [1, 2]를 메모리에 저장한다면, 각각 4개의 슬롯을 필요로 하므로 총 8개의 메모리 슬롯이 필요하다. 이 때도 마찬가지로 단순히 8 개가 아니라 8개의 연속적인 빈 슬롯이 필요하다.
String 은 어떻게 저장할까
앞에서 컴퓨터에서 모든 데이터는 0 과 1 로 변환 가능하다고 한 것처럼 string type 의 데이터도 2 진수로 변환되어 저장된다. 먼저 각 문자는 그에 대응하는 숫자로 mapping 되는 데, 이 규칙을 정해놓은 table 들이 있다.
대표적으로 영어의 각 문자를 수로 mapping 하는 ASCII code 가 있다. ASCII 에서 A 는 65 로 mapping 되고 메모리에 저장될 때 다시 65 는 2 진수로 변환되어 저장된다.
Pointer
메모리 슬롯에는 다른 메모리 슬롯의 address 를 저장할 수 도 있다.
포인터가 멋진 이유는 메모리 슬롯 address 를 직접 저장하지 않고 해당 메모리 슬롯의 address 를 point 하는데 있다.
일반적인 데이터를 저장할 때와는 다르다.
저장하는 메모리 슬롯과 저장할 메모리 슬롯 사이에 있는 슬롯들이 특정 데이터를 저장하고 있어도, 저장할 메모리 슬롯 address 를 포인트 할 수 있다.

컴퓨터 or 프로그램이 메모리 슬롯에 접근하는 operation 의 특성
컴퓨터 또는 프로그램은 메모리 슬롯에 매우 직접적이고 빠르게 접근한다. 메모리 슬롯에 접근하는 operation 이 빠르게 수행되고 비용이 거의 들지 않는다고 이해하면 된다.
저장해놓은 32-bits integer 에 접근하기 위해 4 개의 슬롯에 접근하거나 포인터를 확인하는 작업은 매우 빠르고 비용이 거의 들지 않는다.
